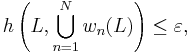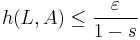Collage theorem
In mathematics, the collage theorem characterises an iterated function system whose attractor is close, relative to the Hausdorff metric, to a given set. The IFS described is composed of contractions whose images, as a collage or union when mapping the given set, are arbitrarily close to the given set. It is typically used in fractal compression.
Contents |
Statement of the theorem
Let 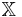 be a complete metric space. Let
be a complete metric space. Let 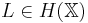 be given, and let
be given, and let 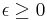 be given. Choose an iterated function system (IFS)
be given. Choose an iterated function system (IFS) 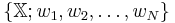 with contractivity factor
with contractivity factor 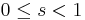 , so that
, so that
where 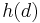 is the Hausdorff metric. Then
is the Hausdorff metric. Then
where A is the attractor of the IFS.
See also
References
- Barnsley, Michael. (1988). Fractals Everywhere. Academic Press, Inc.. ISBN 0-12-079062-9.